Relative Motion – KS3 Tutorial
What is Relative Motion?
Relative motion is how one object appears to move when you compare it to another object.
🔍 Imagine you’re sitting in a car next to another car. If both cars move at the same speed, they look still — but they’re actually moving!
It’s not just about how fast you’re moving — it’s how fast you’re moving compared to another moving thing.
🧍♂️ Imagine This:
You’re walking at 2 m/s. Another student walks past you at 4 m/s in the same direction.
To you, it feels like they’re only moving at 2 m/s (not 4).
That’s relative motion in action.
📗 Why Do We Use Relative Motion?
- To work out how fast things are getting closer or further apart
- To compare moving objects (cars, people, trains, etc.)
- Especially useful in transport, racing, or passing situations
🔄 Two Situations in Relative Motion
🔹 1. Objects moving in opposite directions (e.g., two trains facing each other):
👉 Rule: Add their speeds
📌 Example:
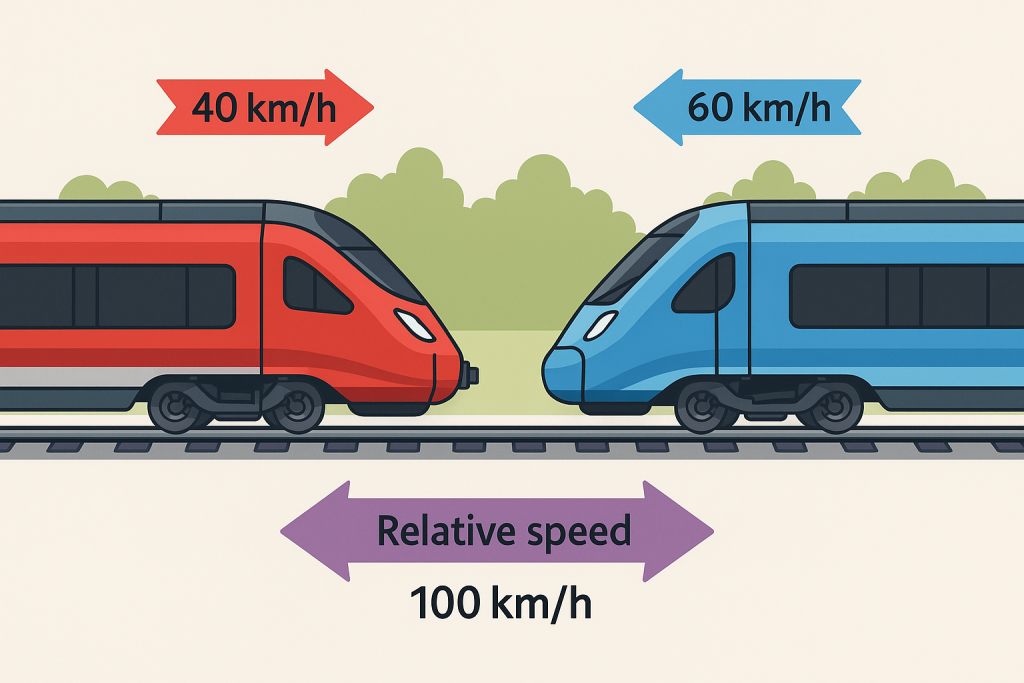
- Train A = 40 km/h
- Train B = 60 km/h (coming toward A)
- Relative speed = 40 + 60 = 100 km/h
➡ They come together faster.
You are on the red train and see the blue train coming toward you.
It looks like the blue train is moving at 100 km/h,
because you are moving at 40 km/h, and the blue train is moving at 60 km/h in the opposite direction.
This is why the relative speed is 40 + 60 = 100 km/h — they come together faster.
🔹 2. Objects moving in the same direction (e.g., car overtaking a tractor):
👉 Rule: Subtract their speeds
📌 Example:
- Car = 30 mph
- Tractor = 20 mph (both moving forward)
- Relative speed = 30 – 20 = 10 mph
➡ The car pulls away slowly.
📊 Summary Chart
| Direction | Rule to Use | Example | Result |
|---|---|---|---|
| Opposite directions | Add the speeds | 30 + 25 | 55 km/h |
| Same direction | Subtract the speeds | 30 – 20 | 10 mph |
🧪 Try It Yourself
- Two cyclists ride towards each other: One at 12 km/h, the other at 8 km/h.
➤ Relative speed = ________
✅ Answer: km/h - A bus (50 km/h) overtakes a scooter (30 km/h).
➤ Relative speed = ________
✅ Answer: km/h
